Speed-To-Fly for a Crosswind Final Glide

At the 1998 Minnesota Soaring Club Safety Meeting the issue arose of how to determine the best L/D and speed to fly when flying in a 25-knot crosswind in four of the club's gliders. I present here a graphical polar analysis which does the job and also illustrates several points.

The Wind Circle

First, consider a typical polar. I've indicated the tangents for both a 10-knot tailwind and for a 10-knot headwind. Notice that they intersect the x-axis at opposite ends of a semicircular arc. I will call this arc the "wind circle."

The Equivalent Crosswind

Well, guess what? You can construct a wind triangle using this idea of a wind circle. Remember, all you need for a wind triangle is a wind vector, a ground track vector, and a heading vector. It turns out the heading vector is just the x-axis, and the ground track vector is based on the ground speed, which is read off the polar now as usual.

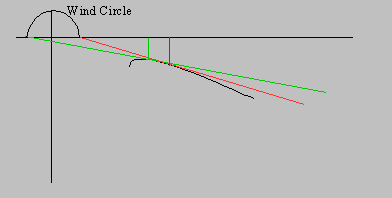
I'll focus first on a headwind. Here I've drawn the exact same tangent, but I've constructed a new, larger, wind circle, and I've added a "track circle" for the ground track:

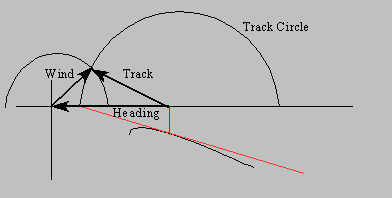
This now says: The performance of my glider in terms of sink rate in the original 10-knot headwind will be identical to its performance in this equivalent crosswind (a stiff blast from 300, roughly). Clearly this is the only wind triangle that can be made from these two circles, but you could imagine an infinite number of triangles based on different sized wind circles, all consistent with this headwind/tangent combination.

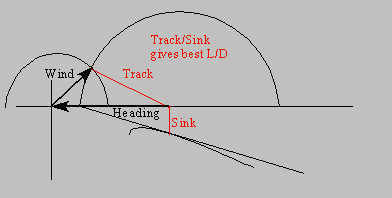
Calculating the Best L/D in a Crosswind

To calculate L/D, we use the length of the TRACK vector divided by the sink, because you always want the ground speed divided by sink rate for L/D:

Note that this works perfectly fine for a tailwind as well. One just has a larger track circle, and now the track vector will ALWAYS be longer than the heading vector.

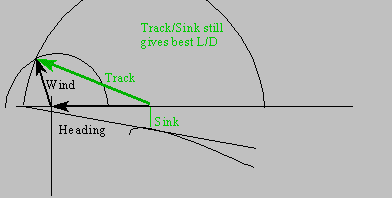
I think it can be proven that you can't get a 90^o intersect for the wind and track vectors to give an "effective" tailwind. (This is because in order to get a 90^o intersect at least one of the arrow bases must be outside the track circle.) Thus, a crosswind with any headwind component at all can never help you!

Finding the Tangent

So far so good, but what if we know the crosswind and want to find the tangent instead of the other way around? As pointed out at our safety meeting, this requires iteration. But you might be surprised how little iteration it takes! I believe that ONE iteration does the trick. My method goes like this:

1) Start by drawing the NO WIND tangent, giving speed "V₀." Add a wind circle for the known wind, and (this is the hard part...) draw track and wind vectors which intersect the wind circle in such as way as to have the known relationship. (Here we are going for a 90 or 270 crosswind.)

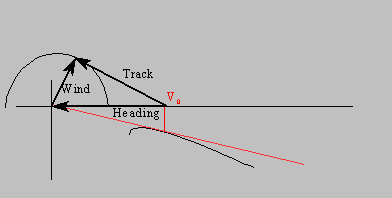
2) Now draw the track circle, find its intersection with the x-axis, and draw a NEW tangent from that point, giving a new speed to fly, V₁, which will be displaced to the right just a bit from V_o.

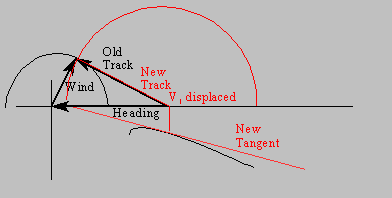
Clearly a crosswind is just like a headwind. Draw the new track vector and measure its length for the L/D calculation.

In principle, you could continue this process, drawing another track vector, track circle, intersection, tangent, etc. But the point I would make is that if you think about it, all future iterations will be between V₀ and V₁. (Because now you have to rotate that wind vector just a hair CCW to reconnect with the right angle at V₁, which will give a slightly smaller effective headwind, which will result in a slightly less steep slope and a slightly smaller V₁, etc., etc.) In fact, the speed to fly will be very close to V₁. Being a knot or two high is the safest idea, anyway. Thus, once through should be plenty.

Lift or Sink: The Effective X-Axis

How does the picture change in lift or sink? Remember that the trick we use with sink, to start the tangent displaced on the vertical axis is really just a way of "faking" the fact that really the polar itself has dropped in sink or risen in lift. Thus, in sink or lift simply use that offset as the "true x-axis" for all your work, and remember that total sink is from the true x-axis, not the one drawn on the polar:

Summary

Headwind and tailwind calculations on a polar are just special cases. In fact, winds from any heading can be considered if you add the ideas of "wind circles" and "track circles." Every crosswind can be thought of as an effective headwind determined by subtracting the length of the track arrow from the length of the heading arrow. It is the track speed which gets divided by total sink rate to give the best L/D.

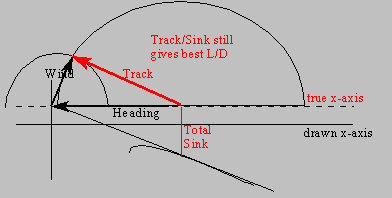
Add some lift or sink and the story changes only in that you would then use that lift or sink line instead of the x-axis for all your circles and intersects.

If you really want to see this the way it looks in space, what you need to do is fold the diagram 90^o along the base of the wind triangle so that the wind-triangle part is flat on your desk while the polar part hangs down the edge. Now that's the real 3-D picture I had in mind at the meeting!

Correct me if I'm wrong...

Happy soaring,

Bob Hanson

hansonr@stolaf.edu